本章主要说明如何对训练过程进行存储,恢复操作。以及在模型长期没有改进时,提前终止训练。
这是几篇与原作不完全相同的教程,转载请说明出处:Gaussic
原作者:Magnus Erik Hvass Pedersen / GitHub / Videos on YouTube
在第三章中,我们使用TensorFlow的API重新构建了网络,并且训练了10000轮次得到了98.7%的测试准确率。然而,在实际训练过程中,模型的结构往往比这更加复杂,数据量也更多,训练10000轮次需要较长的时间。长时间的训练存在多个问题:
- 如果不保存训练过程中的状态,在程序运行完后,整个训练过程被销毁,无法运用到新的数据集上,这样的模型没有意义。
- 如果在训练过程中一旦出现突发情况停止,之前的训练将前功尽弃,必须从头开始训练。
- 如果经过多次的训练,模型的性能不再提升,那么这些训练是没有意义的,如果不提前终止,将浪费大量时间。
事实上,TensorFlow提供了保存和恢复训练的方法,可以避免这类事情的发生。在本章中,我们将继续使用第三章的大部分代码,只做小部分的修改,以实现我们的目的。
载入数据,构建模型
这一部分与第三章相似,但是我们在本章中使用验证集来验证模型性能,因此需要稍作改动。此外,需要用到上一章给出的cnn_helper.py。
from cnn_helper import *
# notebook使用
%load_ext autoreload
%autoreload 2
%matplotlib inline
数据
from tensorflow.examples.tutorials.mnist import input_data
data = input_data.read_data_sets('data/MNIST/', one_hot=True)
print()
print("数据集大小:")
print('- 训练集:{}'.format(len(data.train.labels)))
print('- 测试集:{}'.format(len(data.test.labels)))
print('- 验证集:{}'.format(len(data.validation.labels)))
数据集大小:
- 训练集:55000
- 测试集:10000
- 验证集:5000
data.test.cls = np.argmax(data.test.labels, axis=1)
data.validation.cls = np.argmax(data.validation.labels, axis=1)
神经网络参数
img_size = 28 # 图片的高度和宽度
img_size_flat = img_size * img_size # 展平为向量的尺寸
img_shape = (img_size, img_size) # 图片的二维尺寸
num_channels = 1 # 输入为单通道灰度图像
num_classes = 10 # 类别数目
# 卷积层 1
filter_size1 = 5 # 5 x 5 卷积核
num_filters1 = 16 # 共 16 个卷积核
# 卷积层 2
filter_size2 = 5 # 5 x 5 卷积核
num_filters2 = 36 # 共 36 个卷积核
# 全连接层
fc_size = 128 # 全连接层神经元数
占位符
x = tf.placeholder(tf.float32, shape=[None, img_size_flat], name='x') # 原始输入
x_image = tf.reshape(x, [-1, img_size, img_size, num_channels]) # 转换为2维图像
y_true = tf.placeholder(tf.float32, shape=[None, num_classes], name='y_true') # 原始输出
y_true_cls = tf.argmax(y_true, axis=1) # 转换为真实类别
卷积神经网络
layer_conv1 = tf.layers.conv2d(inputs=x_image, # 输入
filters=num_filters1, # 卷积核个数
kernel_size=filter_size1, # 卷积核尺寸
padding='same', # padding方法
activation=tf.nn.relu, # 激活函数relu
name='layer_conv1') # 命名用于获取变量
net = tf.layers.max_pooling2d(inputs=layer_conv1, pool_size=2, strides=(2, 2), padding='same')
layer_conv2 = tf.layers.conv2d(inputs=net,
filters=num_filters2,
kernel_size=filter_size2,
padding='same',
activation=tf.nn.relu,
name='layer_conv2')
net = tf.layers.max_pooling2d(inputs=layer_conv2, pool_size=2, strides=(2, 2), padding='same')
layer_flat = tf.contrib.layers.flatten(net) # flatten暂时在tf.contrib一层
layer_fc1 = tf.layers.dense(inputs=layer_flat, units=fc_size, activation=tf.nn.relu, name='layer_fc1')
layer_fc2 = tf.layers.dense(inputs=layer_fc1, units=num_classes, name='layer_fc2')
代价、优化器、准确率
y_pred = tf.nn.softmax(layer_fc2) # softmax归一化
y_pred_cls = tf.argmax(y_pred, axis=1) # 真实类别
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=layer_fc2, labels=y_true)
cost = tf.reduce_mean(cross_entropy)
optimizer = tf.train.AdamOptimizer(learning_rate=1e-4).minimize(cost)
correct_prediction = tf.equal(y_pred_cls, y_true_cls)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
获取权重
def get_weights_variable(layer_name):
# 根据给定的layer_name,返回名为'kernel'的变量
with tf.variable_scope(layer_name, reuse=True):
variable = tf.get_variable('kernel')
return variable
weights_conv1 = get_weights_variable(layer_name='layer_conv1')
weights_conv2 = get_weights_variable(layer_name='layer_conv2')
Saver
为了保存神经网络中的变量,我们需要创建一个Saver对象用来存储和检索TensorFlow计算图中的所有变量。我们可以保存训练过程中的所有结果,在这里仅保存最优的结果。
saver = tf.train.Saver() # 用于保存变量
save_dir = 'checkpoints/' # 保存目录
if not os.path.exists(save_dir):
os.makedirs(save_dir)
save_path = os.path.join(save_dir, 'best_validation') # 最佳验证结果保存路径
运行TensorFlow
创建session并初始化
session = tf.Session()
session.run(tf.global_variables_initializer())
优化器的迭代过程
为了测试优化器的性能,需要多添加几个指标,对代码进行相应调整。
train_batch_size = 64
best_validation_accuracy = 0.0 # 当前最佳验证集准确率
last_improvement = 0 # 上一次有所改进的轮次
require_improvement = 1000 # 如果在1000轮内没有改进,停止迭代
# 计算目前执行的总迭代次数
total_iterations = 0
def optimize(num_iterations):
# 保证更新全局变量.
global total_iterations
global best_validation_accuracy
global last_improvement
# 用来输出用时.
start_time = time.time()
for i in range(num_iterations):
total_iterations += 1
# 获取一批数据,运行优化器
x_batch, y_true_batch = data.train.next_batch(train_batch_size)
feed_dict_train = {x: x_batch, y_true: y_true_batch}
session.run(optimizer, feed_dict=feed_dict_train)
# 每100轮迭代输出状态
if (total_iterations % 100 == 0) or (i == num_iterations - 1):
# 计算训练集准确率.
acc_train = session.run(accuracy, feed_dict=feed_dict_train)
# 验证集准确率,为了尽可能重用代码,这个函数会在后面实现
acc_validation, _ = validation_accuracy()
if acc_validation > best_validation_accuracy: # 如果当前验证集准确率大于之前的最好准确率
best_validation_accuracy = acc_validation # 更新最好准确率
last_improvement = total_iterations # 更新上一次提升的迭代轮次
saver.save(sess=session, save_path=save_path) # 将这一次更新保存下来
improved_str = '*' # 标注为找到提升
else:
improved_str = ''
msg = "迭代轮次: {0:>6}, 训练集准确率: {1:>6.1%}, 验证集准确率: {2:>6.1%} {3}"
print(msg.format(i + 1, acc_train, acc_validation, improved_str))
# 如果在require_improvement轮次内未有提升
if total_iterations - last_improvement > require_improvement:
print("长时间未提升, 停止优化。")
break # 跳出循环
end_time = time.time()
time_dif = end_time - start_time
# 输出用时.
print("用时: " + str(timedelta(seconds=int(round(time_dif)))))
计算分类性能
为了重用代码以评估验证集和测试集的性能,需要重构这部分代码:
batch_size = 256
def predict_cls(images, labels, cls_true):
num_images = len(images)
# 为预测结果申请一个数组
cls_pred = np.zeros(shape=num_images, dtype=np.int)
i = 0 # 数据集的起始id为0
while i < num_images:
# j为下一批次的截止id
j = min(i + batch_size, num_images)
# 创建feed_dict
feed_dict = {x: images[i:j, :], y_true: labels[i:j, :]}
# 计算预测结果
cls_pred[i:j] = session.run(y_pred_cls, feed_dict=feed_dict)
# 设定为下一批次起始值.
i = j
# 正确的分类
correct = (cls_true == cls_pred)
return correct, cls_pred
def predict_cls_test(): # 测试集分类结果
return predict_cls(images = data.test.images,
labels = data.test.labels,
cls_true = data.test.cls)
def predict_cls_validation(): # 验证集分类结果
return predict_cls(images = data.validation.images,
labels = data.validation.labels,
cls_true = data.validation.cls)
def cls_accuracy(correct): # 准确率
# 计算总的正确个数
correct_sum = correct.sum()
#计算准确率
acc = float(correct_sum) / len(correct)
return acc, correct_sum
def validation_accuracy(): # optimize()用到的验证集准确率函数
correct, _ = predict_cls_validation()
return cls_accuracy(correct)
测试集性能评估
def print_test_accuracy(show_example_errors=False,
show_confusion_matrix=False):
# 返回测试集的正确情况与预测结果
correct, cls_pred = predict_cls_test()
# 计算准确率,准确数
acc, num_correct = cls_accuracy(correct)
num_images = len(correct)
# 打印准确率.
msg = "测试集准确率: {0:.1%} ({1} / {2})"
print(msg.format(acc, num_correct, num_images))
# 打印部分错误样例.
if show_example_errors:
print("Example errors:")
plot_example_errors(data_test=data.test, cls_pred=cls_pred, correct=correct, img_shape=img_shape)
# 打印混淆矩阵.
if show_confusion_matrix:
print("Confusion Matrix:")
plot_confusion_matrix(cls_true=data.test.cls, cls_pred=cls_pred)
优化前性能:
print_test_accuracy()
测试集准确率: 13.5% (1348 / 10000)
执行10000轮迭代:
optimize(num_iterations=10000)
迭代轮次: 100, 训练集准确率: 81.2%, 验证集准确率: 78.9% *
迭代轮次: 200, 训练集准确率: 85.9%, 验证集准确率: 86.9% *
迭代轮次: 300, 训练集准确率: 93.8%, 验证集准确率: 90.9% *
迭代轮次: 400, 训练集准确率: 92.2%, 验证集准确率: 92.1% *
迭代轮次: 500, 训练集准确率: 93.8%, 验证集准确率: 93.0% *
迭代轮次: 600, 训练集准确率: 95.3%, 验证集准确率: 93.7% *
迭代轮次: 700, 训练集准确率: 90.6%, 验证集准确率: 94.3% *
迭代轮次: 800, 训练集准确率: 98.4%, 验证集准确率: 94.7% *
迭代轮次: 900, 训练集准确率: 96.9%, 验证集准确率: 95.4% *
迭代轮次: 1000, 训练集准确率: 96.9%, 验证集准确率: 95.5% *
迭代轮次: 1100, 训练集准确率: 93.8%, 验证集准确率: 95.7% *
迭代轮次: 1200, 训练集准确率: 98.4%, 验证集准确率: 96.0% *
迭代轮次: 1300, 训练集准确率: 96.9%, 验证集准确率: 95.8%
迭代轮次: 1400, 训练集准确率: 96.9%, 验证集准确率: 96.1% *
迭代轮次: 1500, 训练集准确率: 98.4%, 验证集准确率: 96.3% *
迭代轮次: 1600, 训练集准确率: 98.4%, 验证集准确率: 96.7% *
迭代轮次: 1700, 训练集准确率: 92.2%, 验证集准确率: 96.8% *
迭代轮次: 1800, 训练集准确率: 96.9%, 验证集准确率: 96.9% *
迭代轮次: 1900, 训练集准确率: 100.0%, 验证集准确率: 96.8%
迭代轮次: 2000, 训练集准确率: 98.4%, 验证集准确率: 97.0% *
迭代轮次: 2100, 训练集准确率: 100.0%, 验证集准确率: 97.0% *
迭代轮次: 2200, 训练集准确率: 98.4%, 验证集准确率: 97.4% *
迭代轮次: 2300, 训练集准确率: 96.9%, 验证集准确率: 97.3%
迭代轮次: 2400, 训练集准确率: 96.9%, 验证集准确率: 97.3%
迭代轮次: 2500, 训练集准确率: 96.9%, 验证集准确率: 97.5% *
迭代轮次: 2600, 训练集准确率: 98.4%, 验证集准确率: 97.3%
迭代轮次: 2700, 训练集准确率: 95.3%, 验证集准确率: 97.4%
迭代轮次: 2800, 训练集准确率: 100.0%, 验证集准确率: 97.7% *
迭代轮次: 2900, 训练集准确率: 98.4%, 验证集准确率: 97.7%
迭代轮次: 3000, 训练集准确率: 93.8%, 验证集准确率: 97.8% *
迭代轮次: 3100, 训练集准确率: 98.4%, 验证集准确率: 97.9% *
迭代轮次: 3200, 训练集准确率: 98.4%, 验证集准确率: 97.9%
迭代轮次: 3300, 训练集准确率: 96.9%, 验证集准确率: 97.9%
迭代轮次: 3400, 训练集准确率: 98.4%, 验证集准确率: 97.9%
迭代轮次: 3500, 训练集准确率: 96.9%, 验证集准确率: 97.8%
迭代轮次: 3600, 训练集准确率: 100.0%, 验证集准确率: 98.0% *
迭代轮次: 3700, 训练集准确率: 98.4%, 验证集准确率: 97.8%
迭代轮次: 3800, 训练集准确率: 100.0%, 验证集准确率: 97.9%
迭代轮次: 3900, 训练集准确率: 98.4%, 验证集准确率: 97.9%
迭代轮次: 4000, 训练集准确率: 100.0%, 验证集准确率: 97.7%
迭代轮次: 4100, 训练集准确率: 98.4%, 验证集准确率: 98.1% *
迭代轮次: 4200, 训练集准确率: 98.4%, 验证集准确率: 98.0%
迭代轮次: 4300, 训练集准确率: 100.0%, 验证集准确率: 97.9%
迭代轮次: 4400, 训练集准确率: 98.4%, 验证集准确率: 98.1% *
迭代轮次: 4500, 训练集准确率: 100.0%, 验证集准确率: 98.1%
迭代轮次: 4600, 训练集准确率: 100.0%, 验证集准确率: 97.9%
迭代轮次: 4700, 训练集准确率: 98.4%, 验证集准确率: 98.2% *
迭代轮次: 4800, 训练集准确率: 96.9%, 验证集准确率: 98.2% *
迭代轮次: 4900, 训练集准确率: 100.0%, 验证集准确率: 98.2%
迭代轮次: 5000, 训练集准确率: 100.0%, 验证集准确率: 98.3% *
迭代轮次: 5100, 训练集准确率: 100.0%, 验证集准确率: 98.3%
迭代轮次: 5200, 训练集准确率: 98.4%, 验证集准确率: 98.3%
迭代轮次: 5300, 训练集准确率: 100.0%, 验证集准确率: 98.4% *
迭代轮次: 5400, 训练集准确率: 98.4%, 验证集准确率: 98.3%
迭代轮次: 5500, 训练集准确率: 96.9%, 验证集准确率: 98.4% *
迭代轮次: 5600, 训练集准确率: 98.4%, 验证集准确率: 98.3%
迭代轮次: 5700, 训练集准确率: 98.4%, 验证集准确率: 98.4% *
迭代轮次: 5800, 训练集准确率: 98.4%, 验证集准确率: 98.4% *
迭代轮次: 5900, 训练集准确率: 96.9%, 验证集准确率: 98.4%
迭代轮次: 6000, 训练集准确率: 95.3%, 验证集准确率: 98.4%
迭代轮次: 6100, 训练集准确率: 100.0%, 验证集准确率: 98.3%
迭代轮次: 6200, 训练集准确率: 100.0%, 验证集准确率: 98.5% *
迭代轮次: 6300, 训练集准确率: 100.0%, 验证集准确率: 98.4%
迭代轮次: 6400, 训练集准确率: 100.0%, 验证集准确率: 98.6% *
迭代轮次: 6500, 训练集准确率: 100.0%, 验证集准确率: 98.4%
迭代轮次: 6600, 训练集准确率: 100.0%, 验证集准确率: 98.7% *
迭代轮次: 6700, 训练集准确率: 100.0%, 验证集准确率: 98.7% *
迭代轮次: 6800, 训练集准确率: 100.0%, 验证集准确率: 98.4%
迭代轮次: 6900, 训练集准确率: 100.0%, 验证集准确率: 98.6%
迭代轮次: 7000, 训练集准确率: 96.9%, 验证集准确率: 98.7%
迭代轮次: 7100, 训练集准确率: 98.4%, 验证集准确率: 98.4%
迭代轮次: 7200, 训练集准确率: 100.0%, 验证集准确率: 98.5%
迭代轮次: 7300, 训练集准确率: 98.4%, 验证集准确率: 98.6%
迭代轮次: 7400, 训练集准确率: 98.4%, 验证集准确率: 98.6%
迭代轮次: 7500, 训练集准确率: 98.4%, 验证集准确率: 98.4%
迭代轮次: 7600, 训练集准确率: 100.0%, 验证集准确率: 98.6%
迭代轮次: 7700, 训练集准确率: 100.0%, 验证集准确率: 98.7%
长时间未提升, 停止优化。
用时: 0:13:31
我们发现,在经过6700轮次后,由于性能不再提升,优化器提前停止了迭代,减少了部分的训练时间,而验证集的准确率达到了98.7%。
print_test_accuracy(show_example_errors=True, show_confusion_matrix=True)
测试集准确率: 98.7% (9865 / 10000)
Example errors:

Confusion Matrix:
[[ 973 0 1 0 0 1 2 1 2 0]
[ 0 1127 2 0 0 0 2 1 3 0]
[ 0 1 1021 1 1 0 0 3 4 1]
[ 0 0 1 998 0 7 0 1 3 0]
[ 0 0 1 0 979 0 1 1 0 0]
[ 2 0 0 3 0 885 2 0 0 0]
[ 5 3 0 0 3 5 940 0 2 0]
[ 1 1 6 2 0 0 0 1017 1 0]
[ 3 0 4 2 1 2 0 3 957 2]
[ 2 4 1 4 13 6 0 7 4 968]]

打印权重
weights1 = session.run(weights_conv1)
plot_conv_weights(weights=weights1)
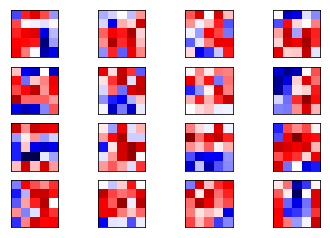
重新初始化
再次重新初始化所有的变量
session.run(tf.global_variables_initializer()) # 重新初始化
print_test_accuracy() # 准确率降回随机
测试集准确率: 19.4% (1937 / 10000)
可见,输出降回了随机的情况。
weights1 = session.run(weights_conv1)
plot_conv_weights(weights=weights1) # 权重也与上面的权重不同
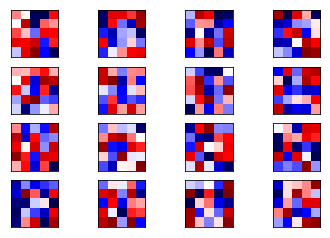
权重也与训练好的模型大不相同。
恢复路径下的变量
现在需要从变量所保存的路径下恢复所有的变量。
saver.restore(sess=session, save_path=save_path) # 现在从保存的目录中重新载入所有的变量
再次计算准确率
# 再次打印测试准确率
print_test_accuracy(show_example_errors=True, show_confusion_matrix=True)
测试集准确率: 98.6% (9864 / 10000)
Example errors:

Confusion Matrix:
[[ 974 0 1 0 0 1 2 0 1 1]
[ 0 1126 3 0 0 0 2 1 3 0]
[ 0 0 1022 1 1 0 0 3 4 1]
[ 0 0 1 1002 0 3 0 1 2 1]
[ 0 0 1 0 980 0 1 0 0 0]
[ 2 0 0 4 0 882 2 0 0 2]
[ 3 2 0 0 3 6 942 0 2 0]
[ 1 3 7 3 0 0 0 1005 1 8]
[ 4 0 6 6 1 3 1 2 946 5]
[ 2 3 2 3 7 4 0 2 1 985]]

可以发现,测试集的准确率达到了98.6%,与前面训练好的模型相差无几。
weights1 = session.run(weights_conv1)
plot_conv_weights(weights=weights1)
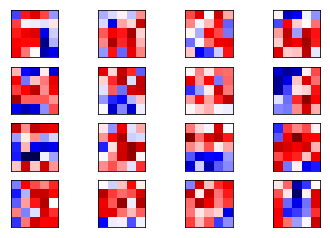
这一次权重和训练过后的就基本相同了,存在轻微不同的原因是原始的模型多训练了1000次。
在重新载入变量后,我们还可以继续优化这些变量。
关闭session
session.close()
